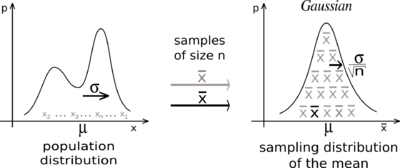「Data distribution」の版間の差分
Vaccipedia.admin (トーク | 投稿記録) |
Vaccipedia.admin (トーク | 投稿記録) |
||
| 37行目: | 37行目: | ||
|} | |} | ||
| − | + | Variance of Binomial data ~ proportion=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{|class="wikitable" style="text-align:center"| | {|class="wikitable" style="text-align:center"| | ||
|- | |- | ||
| 213行目: | 208行目: | ||
</div> | </div> | ||
</div> | </div> | ||
| + | |||
| + | ====Sum of squares==== | ||
| + | In ANOVA, sums of squares in total and in groups are compared. | ||
| + | |||
| + | Sum of squares is the numerator of variance. | ||
| + | :Variance | ||
| + | ::<math>= \frac{\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2}{n-1}</math> | ||
| + | :Sum of square | ||
| + | ::<math>= {\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2}</math> | ||
==Standard Error== | ==Standard Error== | ||
2023年1月18日 (水) 17:43時点における版
Standard deviation and Variance
SD/Variance of Quantitative data ~ mean
| Size | Mean | Standard deviation | Variance | notes | |
|---|---|---|---|---|---|
| Population | [math]\displaystyle{ N }[/math] | [math]\displaystyle{ \mu = \frac{\textstyle \sum_{i=1}^N X_i}{N} }[/math] | [math]\displaystyle{ \sigma=\sqrt{\frac{\sum_{i=1}^N (X_i-\mu)^2}{N}} }[/math] | [math]\displaystyle{ \sigma^2=\frac{\sum_{i=1}^N (X_i-\mu)^2}{N} }[/math] |
|
| Sample | [math]\displaystyle{ n }[/math] | [math]\displaystyle{ \overline{x} = \frac{\textstyle \sum_{i=1}^n x_i}{n} }[/math] | [math]\displaystyle{ s=\sqrt{\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{\color{Red}n-1}} }[/math] | [math]\displaystyle{ s^2=\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{\color{Red}n-1} }[/math] |
|
Variance of Binomial data ~ proportion===
| Size | Proportion | Standard deviation ¶ | Variance ¶ | notes | |
|---|---|---|---|---|---|
| population | [math]\displaystyle{ N }[/math] | [math]\displaystyle{ \pi = \frac{\sum_{i=1}^N X_i}{N} }[/math]
* [math]\displaystyle{ X_i = 0 }[/math] or [math]\displaystyle{ 1 }[/math] |
[math]\displaystyle{ \sigma = \sqrt{\pi (1 - \pi)} }[/math] | [math]\displaystyle{ \sigma^2 = \pi (1 - \pi) }[/math] |
|
| sample | [math]\displaystyle{ n }[/math] | [math]\displaystyle{ p = \frac{\sum_{i=1}^n x_i}{n} }[/math]
* [math]\displaystyle{ x_i = 0 }[/math] or [math]\displaystyle{ 1 }[/math] |
[math]\displaystyle{ \begin{align} s & = \sqrt{\frac{n}{n-1} \cdot p (1 - p)} \\ & \approx \sqrt{p (1-p)} \end{align} }[/math] | [math]\displaystyle{ \begin{align} s^2 & = \frac{n}{n-1} \cdot p (1 - p) \\ & \approx p (1 - p) \end{align} }[/math] |
|
¶ How to derive variance and standard deviation of proportion in population:
Definition of variance of values of in population is [math]\displaystyle{ \frac{\sum_{i=1}^N (X_i - \mu)^2}{N} }[/math] .
Here, [math]\displaystyle{ {\color{Green}\mu} }[/math] is [math]\displaystyle{ {\color{Green}\frac{\sum_{i=1}^N X_i}{n}} }[/math] according to its definition.
This is [math]\displaystyle{ {\color{Green}\pi} }[/math] itself (refer to the above table).
- [math]\displaystyle{ {\color{Green}\mu} = {\color{Green}\frac{\sum_{i=1}^N X_i}{N}} = {\color{Green}\pi} }[/math]
And when we consider [math]\displaystyle{ {\color{Red}\frac{\sum_{i=1}^N X_i^2}{N}} }[/math] , provided that [math]\displaystyle{ X_i = 0 }[/math] or [math]\displaystyle{ 1 }[/math], it leads:
- [math]\displaystyle{ {\color{Red}\frac{\sum_{i=1}^N X_i^2}{N}} = {\color{Green}\frac{\sum_{i=1}^N X_i}{N}} = {\color{Green}\pi} }[/math]
Thus the variance of population proportion can be calculated as follows:
- [math]\displaystyle{ \begin{align} \sigma^2 & = \frac{\sum_{i=1}^N (X_i - {\color{Green}\mu})^2}{N} \\ & = \frac{\sum_{i=1}^N (X_i - {\color{Green}\pi})^2}{N} \\ & = \frac{\sum_{i=1}^N (X_i^2 - 2 {\color{Green}\pi} \cdot X_i + {\color{Green}\pi^2})}{N} \\ & = \frac{\sum_{i=1}^N X_i^2}{N} - 2 {\color{Green}\pi} \cdot \frac{\sum_{i=1}^N X_i}{N} + {\color{Green}\pi^2} \cdot \frac{\sum_{i=1}^N 1}{N}\\ & = {\color{Red}\frac{\sum_{i=1}^N X_i^2}{N}} - 2 {\color{Green}\pi} \cdot {\color{Green}\frac{\sum_{i=1}^N X_i}{N}} + {\color{Green}\pi^2} \cdot \frac{{\color{Orange}\sum_{i=1}^N 1}}{N}\\ & = {\color{Green}\pi} - 2 {\color{Green}\pi} \cdot {\color{Green}\pi} + {\color{Green}\pi^2} \cdot \frac{\color{Orange}N}{N} \\ & = \pi - 2\pi^2 + \pi^2 \\ & = \pi - \pi^2 \\ & = \pi(1-\pi) \end{align} }[/math]
Then standard deviation is also obtained:
- [math]\displaystyle{ \begin{align} \sigma & = \sqrt{\sigma^2} \\ & = \sqrt{\pi(1-\pi)} \end{align} }[/math]
¶ How to derive variance and standard deviation of proportion in sample:
Definition of variance of values in sample is [math]\displaystyle{ \frac{\sum_{i=1}^n (x_i - \bar x)^2}{n-1} }[/math] .
This can be transformed into [math]\displaystyle{ \frac{n}{n-1} \cdot \frac{\sum_{i=1}^n (x_i - \bar x)^2}{n} }[/math] .
Here, [math]\displaystyle{ {\color{Green}\bar x} }[/math] is [math]\displaystyle{ {\color{Green}\frac{\sum_{i=1}^n x_i}{n}} }[/math] according to its definition.
This is [math]\displaystyle{ {\color{Green}p} }[/math] itself (refer to the above table).
- [math]\displaystyle{ {\color{Green}\bar x} = {\color{Green}\frac{\sum_{i=1}^n x_i}{n}} = {\color{Green}p} }[/math]
And when we consider [math]\displaystyle{ {\color{Red}\frac{\sum_{i=1}^n x_i^2}{n}} }[/math] , provided that [math]\displaystyle{ x_i = 0 }[/math] or [math]\displaystyle{ 1 }[/math], it leads:
- [math]\displaystyle{ {\color{Red}\frac{\sum_{i=1}^n x_i^2}{n}} = {\color{Green}\frac{\sum_{i=1}^n x_i}{n}} = {\color{Green}p} }[/math]
Thus the variance of sample proportion can be calculated as follows:
- [math]\displaystyle{ \begin{align} s^2 & = \frac{\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2}{n-1} \\ & = \frac{n}{n-1} \cdot \frac{\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2}{n} \\ & = \frac{n}{n-1} \cdot \frac{\sum_{i=1}^n (x_i - {\color{Green}p})^2}{n} \\ & = \frac{n}{n-1} \cdot \frac{\sum_{i=1}^n (x_i^2 - 2 {\color{Green}p} \cdot x_i + {\color{Green}p^2})}{n} \\ & = \frac{n}{n-1} \left ( \cdot \frac{\sum_{i=1}^n x_i^2}{n} - 2 {\color{Green}p} \cdot \frac{\sum_{i=1}^n x_i}{n} + {\color{Green}p^2} \cdot \frac{\sum_{i=1}^n 1}{n} \right ) \\ & = \frac{n}{n-1} \left ( {\color{Red}\frac{\sum_{i=1}^n x_i^2}{n}} - 2 {\color{Green}p} \cdot {\color{Green}\frac{\sum_{i=1}^n x_i}{n}} + {\color{Green}p^2} \cdot \frac{{\color{Orange}\sum_{i=1}^n 1}}{n} \right ) \\ & = \frac{n}{n-1} \left ( {\color{Green}p} - 2 {\color{Green}p} \cdot {\color{Green}p} + {\color{Green}p^2} \cdot \frac{\color{Orange}n}{n} \right ) \\ & = \frac{n}{n-1} \left ( p - 2p^2 + p^2 \right ) \\ & = \frac{n}{n-1} \left ( p - p^2 \right ) \\ & = \frac{n}{n-1} \cdot p(1-p) \end{align} }[/math]
Here, if [math]\displaystyle{ n }[/math] is large enough, we can ignore [math]\displaystyle{ \frac{n}{n-1} }[/math] from the calculation.
- [math]\displaystyle{ s^2 \approx p(1-p) }[/math]
Then standard deviation is also obtained:
- [math]\displaystyle{ \begin{align} s & = \sqrt{s^2} \\ & = \sqrt{\frac{n}{n-1} \cdot p(1-p)} \\ & \approx \sqrt{p(1-p)} \end{align} }[/math]
Sum of squares
In ANOVA, sums of squares in total and in groups are compared.
Sum of squares is the numerator of variance.
- Variance
- [math]\displaystyle{ = \frac{\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2}{n-1} }[/math]
- Sum of square
- [math]\displaystyle{ = {\sum_{i=1}^n (x_i - {\color{Green}\bar x})^2} }[/math]
Standard Error
If we repeated infinite times of sampling from the population with sample size of [math]\displaystyle{ n }[/math] every time ([math]\displaystyle{ n }[/math] is large enough), no matter what the population distribution was, those infinite number of sample means follow normal distribution with mean identical to population mean [math]\displaystyle{ \mu }[/math], and variance derived from population variance [math]\displaystyle{ \frac{\sigma^2}{n} }[/math] (not population variance [math]\displaystyle{ \sigma^2 }[/math]itself). This is central limit theorem.
|
Derivation of [math]\displaystyle{ \frac{\sigma^2}{n} }[/math] needs far advanced mathematics like Maclaurin expansion, characteristic function or moment-generating function. |
Hence the standard deviation of sample means is derived from the square root of its variance —— [math]\displaystyle{ \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}} }[/math].
This standard deviation of sample means [math]\displaystyle{ \frac{\sigma}{\sqrt{n}} }[/math] is defined as Standard error.
In reality, God knows the population mean [math]\displaystyle{ \mu }[/math] and population standard deviation [math]\displaystyle{ \sigma }[/math], thus only way to utilize standard error is to assume sample standard deviation would be close to population standard deviation as follows:
[math]\displaystyle{ Standard\ error \approx \frac{s}{\sqrt{n}} }[/math], where [math]\displaystyle{ s }[/math] = sample standard deviation
| Standard error | notes | |
|---|---|---|
| mean | [math]\displaystyle{ \begin{align} SEM & = \frac{\sigma}{\sqrt{N}} \\ & \approx \frac{s}{\sqrt{n}} \end{align} }[/math] |
|
| proportion | [math]\displaystyle{ \begin{align} SE_p & = \frac{\sigma}{\sqrt{N}} = \sqrt{\frac{\pi (1-\pi)}{N}} \\ & \approx \frac{s}{\sqrt{n}} = \sqrt{\frac{p (1-p)}{n}} \end{align} }[/math] |
Standard Error and Confidence Interval
When sample size is large enough and assumed to follow normal distribution
According to Central Limit Theorem, distribution of sample means follow normal distribution with mean of [math]\displaystyle{ \sigma }[/math] (population mean) and standard deviation of [math]\displaystyle{ \frac{\sigma}{\sqrt{n}} }[/math].
The mean of one single sample will lie somewhere within the distribution of sample means around their mean = [math]\displaystyle{ \sigma }[/math] (population mean!) with standard deviation of [math]\displaystyle{ \frac{\sigma}{\sqrt{n}} }[/math].
As a simple rule, in normal distribution, each range of ±[math]\displaystyle{ k }[/math] SD contains the following proportion total values.
| ±[math]\displaystyle{ k }[/math] SD | Proportion |
|---|---|
| ±1 SD | 68.2% |
| ±1.96 SD | 95 % |
| ±2 SD | 95.4% |
| ±2.58 SD | 99 % |
| ±3 SD | 99.7% |
We cannot estimate how far a single sample mean [math]\displaystyle{ \bar{x} }[/math] is from the true mean of sample means = population mean [math]\displaystyle{ \sigma }[/math],
but we can estimate the probability that a certain range of the distribution of a single sample mean contains the true mean of sample means = population mean [math]\displaystyle{ \sigma }[/math] according to above table.
The standard deviation of sample means = Standard Error is [math]\displaystyle{ \frac{\sigma}{\sqrt{n}} }[/math],
and it can be approximate by using the standard deviation of a single sample mean [math]\displaystyle{ s }[/math] as [math]\displaystyle{ \frac{s}{\sqrt{n}} }[/math].
Thus, [math]\displaystyle{ \bar{x}\ \pm\ k \frac{s}{\sqrt{n}} }[/math] is the range of distribution of a single sample mean [math]\displaystyle{ \bar{x} }[/math] and its corresponding proportion is the probability that the range contains [math]\displaystyle{ \sigma }[/math].
[math]\displaystyle{ \bar{x}\ \pm\ 1.96 \frac{s}{\sqrt{n}} }[/math] is 95% Confidence Interval, [math]\displaystyle{ \bar{x}\ \pm\ 2.58 \frac{s}{\sqrt{n}} }[/math] is 99% Confidence Interval.
When sample size is small (roughly <30) and assumed to follow t distribution
We have to refer to t-distribution table instead of normal distribution table (Z table),
as well as take into account of degrees of freedom, [math]\displaystyle{ n-1 }[/math].
Find out the relevant coefficient [math]\displaystyle{ k }[/math] of [math]\displaystyle{ \bar{x}\ \pm\ k \frac{s}{\sqrt{n}} }[/math] from t-distribution table by using desired CI range and degrees of freedom.